Ray Tracer: Hello world

Ray tracing is a complex subject. It needs reasonable amount of mathematics to write even a simple one. But that kind of simple one still generates awesome output. The basic theory is to simulate the travel of light rays from one or more light sources to the eye, subjecting to reflections, refraction and deflections by various objects through its way. To reduce the computational complexity a view is assumed in-front of eye (or camera) and calculates the color of each pixel in the view, based on the amount and hue of the light that may arrive there.

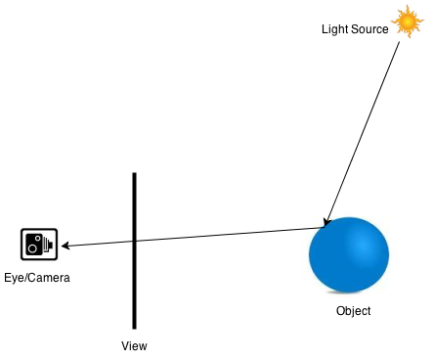
Sphere rendered with ray tracing

A vector class is essential to write a ray tracer.

class vec
{
public:
    vec()                   { x = y = z = 0; }
    vec(double _x, double _y, double _z) { x = _x; y = _y; z = _z; }

    vec operator-(vec& rhs) { return vec(x - rhs.x, y - rhs.y, z - rhs.z); }
    vec operator-()         { return vec(-x, -y, -z); }
    vec operator+(vec& rhs) { return vec(x + rhs.x, y + rhs.y, z + rhs.z); }
    vec operator*(double t) { return vec(x * t, y * t, z * t); }
    double dot(vec& r)      { return x * r.x + y * r.y + z * r.z; }
    vec cross(vec& r)       { return vec(y * r.z - z * r.y, z * r.x - x * r.z, 

                                     x * r.y - y * r.x); }
    double length()         { return sqrt(x * x + y * y + z * z); }
    bool is_equal(vec& r, double eps) { return abs(x - r.x) < eps && abs(y - r.y) < eps 

                                               && abs(z - r.z) < eps; }

    void normalize()
    {
        double d = length();
        x /= d;
        y /= d;
        z /= d;
    }

    static double angle(vec v1, vec v2) { return acos(v1.dot(v2) 

                                                / (v1.length() * v2.length())); }

    double x;
    double y;
    double z;
};

Our first attempt is to trace a sphere illuminated by one omnidirectional light source. For that, this handy function is also required.

bool IntersectLineAndSphere(vec a, vec u, vec S, double r, double& t)
{
    // Line R = a + u*t
    // Sphere center S with radius r. x*x + y*y + z*z = r*r
    // To find the intersection point of ray and the sphere substitute ray on 
    // circle and solve 
    // the quadratic equation for minimum positive t.
    double A = 1;
    double B = 2 * (u.x * (a.x - S.x) + u.y * (a.y - S.y) + u.z * (a.z - S.z));
    double C = (a.x - S.x) * (a.x - S.x) + (a.y - S.y) * (a.y - S.y) 
               + (a.z - S.z) * (a.z - S.z) - r * r;
    double D = B * B - 4 * A * C;
    if (D >= 0)
    {
        double t1 = (-B + sqrt(D)) / 2;
        double t2 = (-B - sqrt(D)) / 2;
        // assuming t1 > 0 && t2 > 0 for this specific setup and as t1 >= t2
        t = t2;
        return true;
    }
    return false;
}

Rays (straight line) are represented in parametric form R = a + ut or x = x0 + dx * t, y = y0 + dy * t, z = z0 + dz * t where t is the parameter that vary along the line. Above function returns the parameter value at the nearest intersection point.

Step 1

Lets forget the light source. Just check where the sphere is.

void Trace(CDC* pDC)
{
    const double PI = 3.14159;
    const double eps = 0.001;

    // Eye or camera
    vec e(0, 0, 0);

    // View port
    vec vp0(-200, -200, 200);
    int vpcx = 400;
    int vpcy = 400;

    // Sphere
    vec S(0, 0, 450);
    double r = 300;

    for (int vpy = vp0.y; vpy < vp0.y + vpcy; ++vpy)
    {
        for (int vpx = vp0.x; vpx < vp0.x + vpcx; ++vpx)
        {
            // For each pixel in view port, the unit vector of ray is
            vec u(vpx - e.x, vpy - e.y, vp0.z - e.z);
            u.normalize();

            int color;
            double t;
            if (IntersectLineAndSphere(e, u, S, r, t))
                color = 100;
            else
                color = 0;

            pDC->SetPixel(vpcx / 2 - vpx, vpcy / 2 - vpy, RGB(color, color, color));
        }
    }
}

Step 2

Easily decorate the background with a checkerboard pattern.

void Trace(CDC* pDC)
{
    ...

    for (int vpy = vp0.y; vpy < vp0.y + vpcy; ++vpy)
    {
        for (int vpx = vp0.x; vpx < vp0.x + vpcx; ++vpx)
        {
            ...

            double t;
            if (IntersectLineAndSphere(e, u, S, r, t))
            {
                 int color = 100;
                 pDC->SetPixel(vpcx / 2 - vpx, vpcy / 2 - vpy
                               , RGB(color, color, color));
            }
            else // no intersection
            {
==>              bool dark = (int)(vpx - vp0.x) / 8 % 2 != (int)(vpy - vp0.y) / 8 % 2;
==>              pDC->SetPixel(vpcx / 2 - vpx, vpcy / 2 - vpy

                               , dark ? 0x0 : 0x202020); // grid
            }
        }
    }
}

Step 3

The sphere is illuminated by the ambient light only. i.e. each point on sphere has a constant brightness value. That light is emitted radially. So amount of light coming from the points at boundary is less than that near the center.

void Trace(CDC* pDC)
{
    ...

    for (int vpy = vp0.y; vpy < vp0.y + vpcy; ++vpy)
    {
        for (int vpx = vp0.x; vpx < vp0.x + vpcx; ++vpx)
        {
            ...

            double t;
            if (IntersectLineAndSphere(e, u, S, r, t))
            {
                 vec vi = e + u * t; // intersection point
                 vec vn = (S - vi) * (1 / r); // surface normal
                 vn.normalize();

==>              double c = (PI / 2 - abs(vec::angle(vn, u))) / (PI / 2) * 256;
==>              int color = min(c / 3, 255);
                 pDC->SetPixel(vpcx / 2 - vpx, vpcy / 2 - vpy, RGB(color, color, color));
            }
            else // no intersection
            {
                 ...
            }
        }
    }
}

Step 4

Lights ON. Check whether the light hits the point that we are interested on. Calculate the amount of light that is reflected towards the selected pixel in the view port. Ambient light turned off to see the reflected light only. Various magic numbers are required to tune the light.

void Trace(CDC* pDC)
{
    ...
    // Omnidirectional Light
    vec L(-400, 400, -600);
    for (int vpy = vp0.y; vpy < vp0.y + vpcy; ++vpy)
    {
        for (int vpx = vp0.x; vpx < vp0.x + vpcx; ++vpx)
        {
             // For each pixel in view port, the unit vector of ray is
             vec u(vpx - e.x, vpy - e.y, vp0.z - e.z);
             u.normalize();
             double t = 0;
             if (IntersectLineAndSphere(e, u, S, r, t))
             {
                  vec vi = e + u * t; // intersection point
                  vec vn = (S - vi) * (1 / r); // surface normal
                  vn.normalize();
                  int color = 0;
                  // Check if light hits this point.

                  // Unit vector of light
                  vec uL = vi - L;
                  uL.normalize();
                  if (IntersectLineAndSphere(L, uL, S, r, t))
                  {
                      vec vL1 = L + uL * t; // nearest point to the light
                      if (vL1.is_equal(vi, eps)) // light hits here
                      {
                          // reflected light
                          vec vr = vn * uL.dot(vn) * 2 - uL;
                          double c = (PI - abs(vec::angle(u, vr))) / PI * 256;
                          c = c * c / 256 + c * c * c / 256 / 500;
                          color += min(c / 1.5, 255);
                       }
                   }

                   pDC->SetPixel(vpcx / 2 - vpx, vpcy / 2 - vpy, RGB(color, color, color));
              }
              else // no intersection
              {
                   ...
              }
         }
     }
}

Step 5

Ambient + Reflection